Power Tower Fractal

함수를 처음 배울때, ‘정의역 (domain)’이나 ‘치역 (range)’과 같은 용어들을 배우게된다. 이번 포스팅에서는 ‘정의역의 형태’를 다뤄볼 생각이다.

먼저 질문 몇가지 :

- - Q1-1. \(x^2\)의 정의역은 무엇인가?
  - Q1-2. 복소평면에서 \(x^2\)의 정의역의 원소는 검정색으로, 정의역이 아닌 원소는 흰색으로 나타내어라.
  - Q2-1. \(\frac{1}{x}\)의 정의역은?
  - Q2-2. 복소평면에서 \(\frac{1}{x}\)의 정의역의 원소는 검정색으로, 정의역이 아닌 원소는 흰색으로 나타내어라.

첫번째 문제부터 살펴보자. \(x^2\)는 xy평면상에서 포물선 그래프를 그리며, 그것은 어디에서도 끊김이 없이 부드럽게 이어진다. 즉, 어떤 \(x\)에 대해서도 \(x^2\)의 값은 잘 정의되며, 따라서 \(x^2\)의 정의역은 ‘실수 전체’이다.

그런데 이와 같은 논의는 애초부터 ‘\(x\)는 실수이다’는 사실을 암묵적으로 전제하고 있다. … 굳이 그럴 필요가 있을까? \(x\)가 복소수라면 \(x^2\)은 복소수 \(x\)를 두번 곱한 어떤 복소수가 되는 것이고, 그 숫자 또한 \(x\)가 어떤 값을 가지던 잘 정의되는 수이다. 따라서, 별다른 조건이 없다면 ‘\(x^2\)의 정의역은 복소수 전체’라 해도 아무 문제가 없다¹. 따라서, Q1-2의 답을 그림으로 나타내면 다음과 같다 :

좀 허탈하게 느껴질지도 모르겠지만, 복소평면상에서 \(x^2\)의 정의역을 검게 칠한다는 것은 그저 복소평면 전체를 검게 칠하는 것이다.

그렇다면 \(\frac{1}{x}\)의 정의역은 무엇인가? \(x\)가 임의의 복소수라면 \(\frac{1}{x}\)은 그 함수의 역수에 해당하는 복소수이다. \(x\)가 \(0\)이 아닌이상 모든 \(x\)에 대한 역수 – 즉 \(\frac{1}{x}\)의 값은 수학적으로 잘 정의되며, 따라서 Q2-2의 답은 다음과 같다 :

복소평면에서 \(\frac{1}{x}\)가 어느 하나의 값으로 정의되지 않는 지점은 원점 밖에 없으며, 따라서 문제에 따라 해당부분을 하얗게 칠한다면 위와같이 원점에만 하얀색 점 하나가 칠해져 있는 형태가 되는 것이다.

다른 예로, \(\frac{1}{x^2+1}\) 같은 경우는 분모를 \(0\)으로 만드는 \(x\)가 \(\pm i\)이므로 이 경우에 해당하는 정의역을 앞선 방식으로 그린다면 :

필자는 고등학교 수준의 함수를 사용하여 뭔가 복잡하고 멋있는 형탤를 만들수는 없을까 고민했지만, 이 이상의 방안이 잘 떠오르지 않았다. 이런 너무나도 뻔하고 재미없어 보이는 이런 그림을 그리는 것은, 사실 복소평면에서 ‘Power Tower 함수’라 불리우는 다음과 같은 함수의 정의역을 보여드리기 위함이다 : \[f(x) = x^{x^{x^{x^{⋰}}}}\]

‘WolframAlpha’라는 사이트 (이하 W.A.)에서 몇몇 지점에 대한 \(f(x)\)의 값을 구해보자. 먼저 \(f(x)\)의 값은 1이다 : \[1^{1^{1^{1^{⋰}}}}=1\]

필자는 W.A.에서 \(1\)이 \(7\)번 쌓아진 경우에 대해서 계산해보았는데, \(1^1=1\)이기 때문에 밑을 \(1\)로하고 그것을 지수자리에 아무리 계속해서 올려도 그 수는 당연히 \(1\)을 유지하는 것이다.

\(f(2)\)의 값은 어떨까? W.A.에서 해보면 \(2^{2^{2^{2^{2}}}}\)는 약 \(2.003 \times 10^{19728}\) 정도로 계산된다. … \(2\)를 다섯번만 쌓아도, 그 수는 자릿수만 19,000개가 넘어간다! 당연히 이 과정을 무한히 하면 그 수는 급격히 발산한다 : \[2^{2^{2^{2^{⋰}}}}=\infty\]

즉, \(x=2\)에서 Power Tower 함수는 어느 하나의 값으로 정의 되지 않는다.

그렇다면 허수 \(i\)에 대한 값 \(i^{i^{i^{i^{⋰}}}}\)의 계산결과는 어떨까? 필자는 이 포스팅에서 이것이 어떻게 계산되는지를 설명할 생각이 없다. 대신, 그저 프로그램에 넣고 돌려보자 (예상밖으로 W.A.가 이런 연산을 해내지 못해서, GeoGebra Calculator를 사용하였다.) :

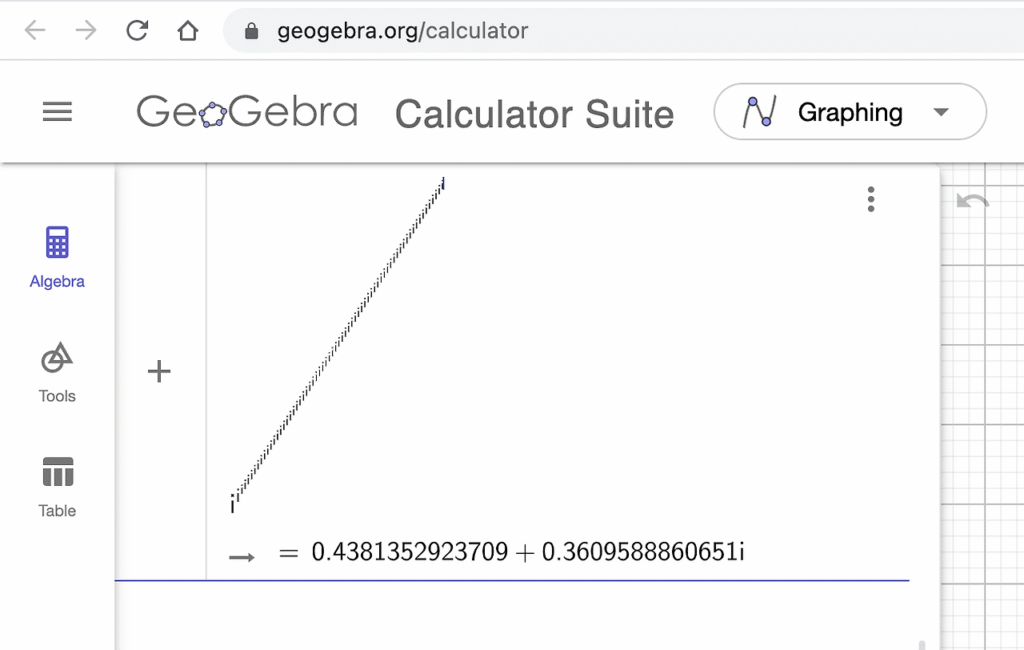
관심이 있으신 분들은 GeoGebra Calculator 사이트에 가셔서 원하는 높이까지 계산해 보실 수 있다. 해보면, \(i^{i^{i^{i^{⋰}}}}\)의 값은 \(0.438+0.361i\)정도로 수렴한다는 것을 알 수 있다.

앞선 결과들을 고려하면, \(x\)가 \(1\), \(2\), \(i\)일때의 정의역은 다음과 같이 표시 되어야 한다 (나머지 부분은 아직 알 수 없으므로 검정과 흰색이 아닌 노란색으로 채웠다):

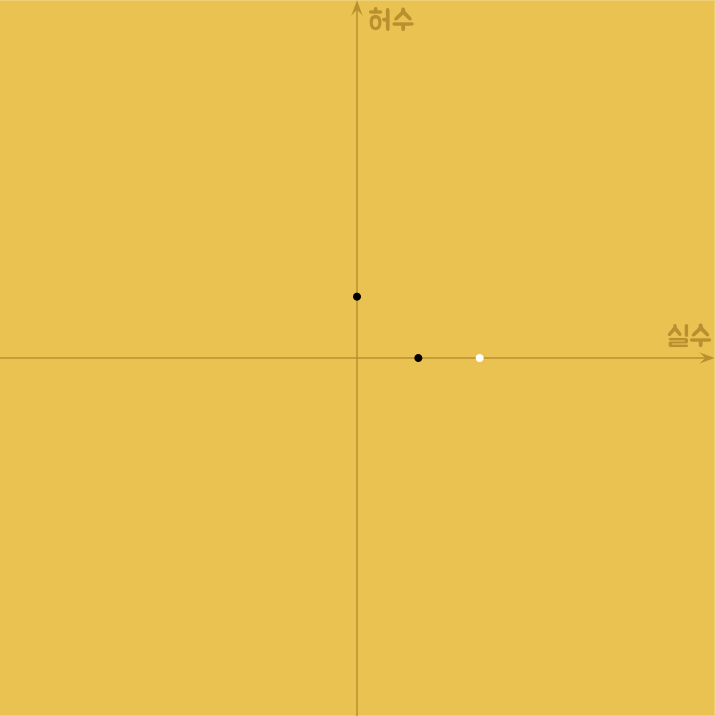
그리고 복소평면상의 나머지 부분까지 다 채운 아래 그림이 함수 \(x^{x^{x^{x^{⋰}}}}\)의 정의역이고, 이것을 ‘Power Tower Fractal’이라 부르기로 하자² :

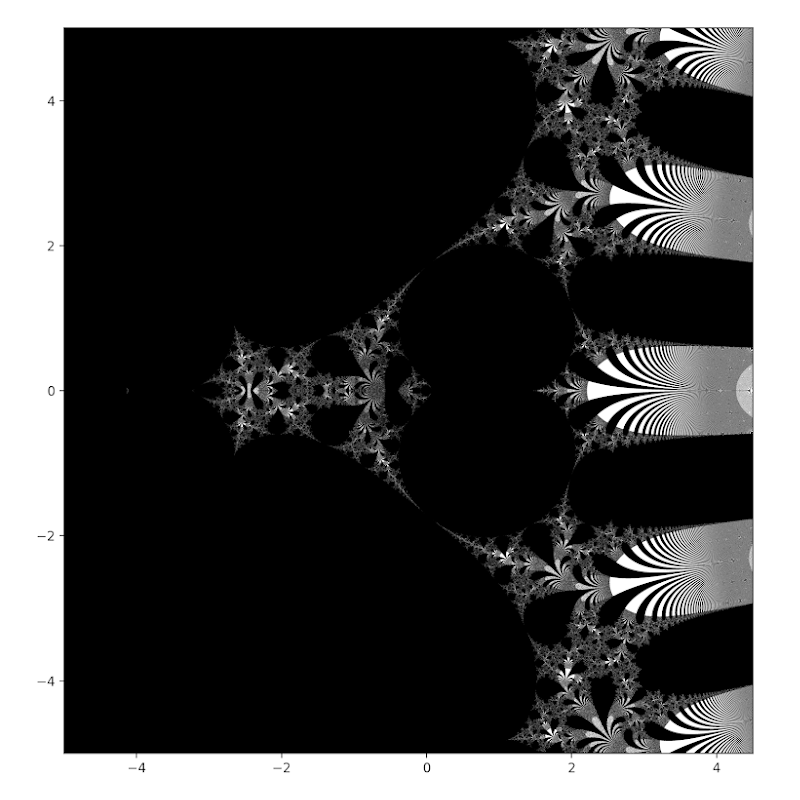
갑자기 이런 그림이 나타나는것에 너무 큰 비약을 느끼실지도 모르겠다. 그런 느낌은 필자도 마찬가지다. 심지어 인류 역사상 가장 위대한 수학자 중 한명인 오일러조차 – 1778년 출간된 그의 논문³에서 ‘아직 이 함수에 대해서는 깊은 이해에 도달하지 못했기 때문에 그것들의 특별한 성질에 대해 논하는 것의 별 의미가 없다’고 기술하고 있으며, 2017년에 출간된 아일랜드 더블린 대학교 수학과 명예교수인 Perter Lynch 의 논문⁴에도, 이 함수에는 ‘풀리지 않은 흥미로운 질문들이 많이 남아있으며’, ‘이러한 수학적 구조속에는 배울만한 내용들이 산적해있다’고 쓰여 있다. 이것을 수식을 이용해서 해석적으로 푼 사람, 혹은 풀 수 있는 사람은 아마 없을 것이다. 하지만 우리는 컴퓨터의 힘을 빌릴 수 있었기 때문에 단순한 몇줄의 코딩으로 그 형태를 그릴 수 있었던 것이다. 실제 인류역사에서 이러한 복잡한 정의역 형태를 처음 본것은 컴퓨터가 등장한 20세기 중후반 이었으며, 그 모습은 다음과 같았다⁵ :

사람들은 발견자의 이름을 따서, 이것을 ‘Mandelbrot Set’이라고 부른다. YouTube에 ‘Mandelbrot Zoom’이고 검색하면 수 없이 많은 영상을 볼 수 있는데, 이는 전체의 형태가 끝없이 반복되는 ‘자기닮음 구조’를 가지고 있으며, 사람들은 이를 ‘프랙탈 구조’라 부른다. 필자는 Power Tower Fractal을 그리는 과정에서, Mandelbrot Set과의 공통점과 차이점들을 발견 할 수 있었다. 그것 하나하나는 엄밀하게 증명되었다기 보다는 관찰에 근거한 예측의 수준인데, 그 중 몇가지를 정리해 보았다 :

Conjecture #1. Power Tower Fractal은 ‘연결된 집합’이다.

Mandelbrot 집합은 ‘열결된 집합’이다. 즉, 함수가 수렴하는 검정색 부분이 모두 연결되어있다는 뜻이다. 학자들이 그 사실을 어떻게 증명했는지는 모르겠으나, 필자는 Power Tower Fractal 또한 동일한 성질을 가지고 있다고 예상한다.

예를들어, 위 이미지에서 붉은색 표시를 한 부분은, 이런 큰 스케일로 봐서는 끊어진 곳인지 아닌지 알 수가 없다. 하지만 충분히 확대를 하면, 거시적으로는 보이지 않는 미세한 ‘필라멘트’로 연결되어있을 것이라는 것이 필자가 코딩하는 과정에서 느낀 점이다. 또한, 연두색으로 표시한 부분에도 아주 미세하게 발산하는 부분이 존재한다. 과연 이 부분은 다른 발산영역과 연결되지 않고 독립적으로 존재하는 부분일까? 너무 근거가 부족해서 이런 예상을 내놓는것에 마음이 상당히 불편하지만, Mandelbrot Set가 그렇듯 연결되어 있을것이라는 것이 필자의 예상이다.

Conjecture #2. Power Tower Fractal에는 명확한 경계를 가지는 부분이 존재한다.

필자는 Mandelbrot Set은 어느 지역에서도 수렴과 발산의 명확한 경계를 찾을 수 없는 것으로 알고있다. 유튜브에 수없이 많은 Mandelbrot Set 확대 영상이 있지만, 그 속에서도 정확한 경계가 나타나는 부분을 찾을 수는 없다. 하지만 이 부분에서 Mandelbrot Set과 Power Tower Fractal에 차이점이 존재하는 것이 아닌가 싶다.

Power Tower Fractal 구조를 표현하자면, 얼음이나 눈결정 같이 미세한 구조가 어떤 ‘줄기’ 형태의 끝에 매달려 있는것 같은 형태이다. 그런데 이 ‘줄기’ 부을 충분히 확대해보면 직선형태가 나타난다⁶ :

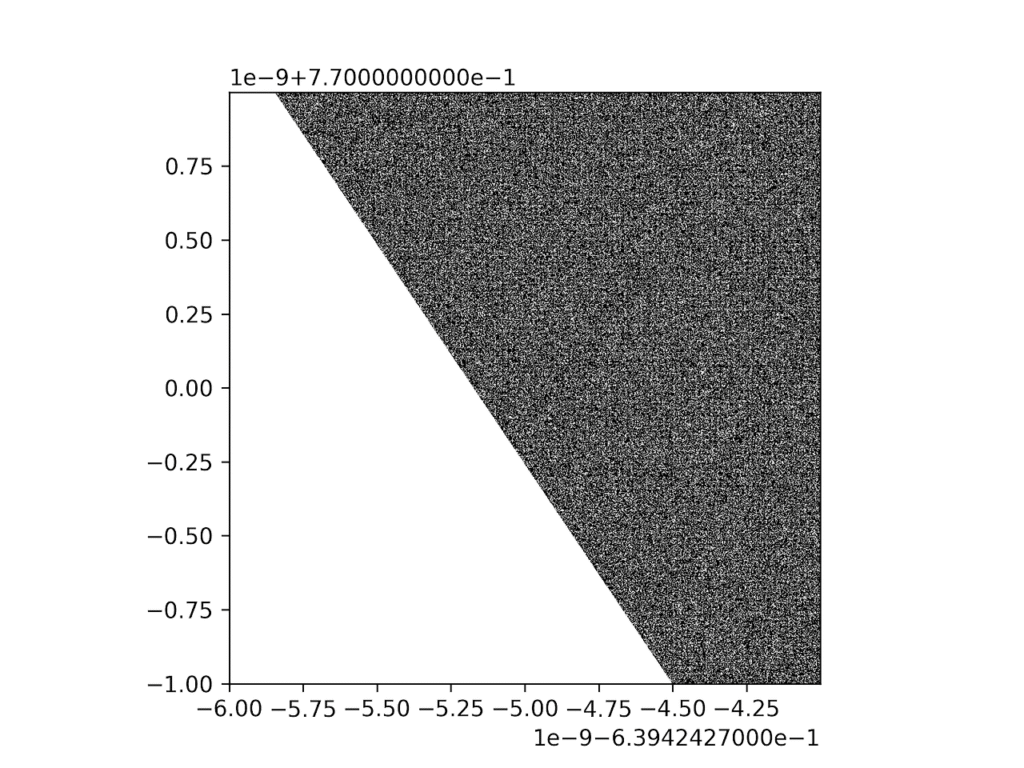
즉, 그 ‘줄기’부분에는 프랙탈 구조가 없는 명확한 경계를 가지는 것이 아닌가 싶은 예상이 든다.

물론 이는 필자의 예상일 뿐이다. 위 이미지는 특정부위를 원래 보다 10⁹배 확대한것인데, 경계를 10⁹⁰⁰배 정도 확대하면 어떤 다른 구조가 나올지는 잘 모르겠다.

Conjecture #3. Power Tower Fractal은 프랙탈 구조를 가진다.

너무나 당연한 말인것 같지만, 필자가 직접 증명을 한적도- 혹은 누군가가 증명한것을 본적도 없기 때문에 나는 이것을 여전히 ‘예측’이라 부를 수 밖에 없다. 즉, 필자는 Power Tower Fractal이 ‘자기닮음’구조를 가졌으며, 무한히 확대해도 수렴/발산의 명확한 경계를 찾을 수 없는 지역들이 존재한다고 예상한다.

그런데 Power Tower Fractal의 일부를 실제로 확대해보면, 그 사실이 너무나 명확한 것 같아 굳이 증명할 필요가 있을까 싶을 정도이다⁷ :

■

필자는 복소수를 포함하는 상위 수체계가 있다는 사실을 알고 있지만, 아직 공부가 부족해 그것이 정확히 무엇인지는 모른다. \(x^2\)의 정의역이 과연 복소수까지로 한정되어야 할 이유가 있을까? 아마도, 확장 가능한 모든 수체계가 그 정의역 일 것이다.[^]
🔗파이썬 코딩[^]
De formulis exponentialibus replicatis (Leonhard Euler, 1778)[^]
The Fractal Boundary of the Power Tower Function (Peter Lynch, 2017) [^]
https://en.wikipedia.org/wiki/Mandelbrot_set#/media/File:Mandel_zoom_00_mandelbrot_set.jpg (물론, 초기에 바로 이런 고해상도의 계산을 하지는 못했다.) [^]
(x,y) = (-0.639424275, 0.77) 부위를 10⁹배 확대하였다.[^]
🔗 파이썬 코드 링크[^]