본 포스팅은 다음 포스팅 내용과 밀접하게 연관됩니다 :
본 포스팅을 읽기 전이나 후에 이 둘을 함께 공부하기를 권장합니다.
$xy$평면 상에서 정의되는 임의의 함수 $f(x,y)$가 어떤 임의의 점$P$ 부근에서 어떻게 변하는지를 보기위해선 다음과 같은 chain rule을 쓰면 된다 : $$df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy \tag{1}$$
이를 gradient $\nabla$를 써서 표시하면 : $$df=\nabla f \cdot d\vec{s} \tag{1.5}$$
나는 종종 식$(1)$에 대한 혼란을 느꼈고, 이는 chain rule 전반에 대한 혼란으로 이어졌다. 내가 느낀 혼란은 이런것이다 — 교과서에서 뭔가를 설명함에 있어 좌표계를 쓴다면, 당연히 직교좌표계에서 시작한다. 사실 따지고 보면, 일반상대론을 배우지 않는 이상 학부수준에서 ‘직선 좌표계’가 ‘직교 좌표계’가 아닌 경우는 대단히 드물다. 시스템의 대칭성을 잘 다루기위해 구면좌표계나 원통좌표계를 사용하지 않는 이상, 두 직선 축으로 이루어진 좌표계를 쓸때면 항상 그 둘이 직교하는 형태를 택한다. 그런 상황 속에서 나는, 무의식적으로 식$(1)$의 형태가 직교좌표계에서만 성립한다고 느꼈던것 같다. 마치 피타고라스의 정리 $a^2+b^2=c^2$은 직각삼각형에서만 참인것처럼 말이다.
하지만 그렇지 않다. chain rule은 어떤 basis에 대한 성분을 나타내는 대단히 일반적인 표현이라서, 서로 직교하지 않는 축들로 이루어진 어떤 임의의 좌표계 $(x^1, x^2)$에서도 식$(1)$은 성립한다 : $$df = \frac{\partial f}{\partial x^1} dx^1 + \frac{\partial f}{\partial x^2} dx^2 \tag{2}$$
나는 최근, 고등과학원KIAS 이필진 교수님이 2022년 겨울에 했던 <From Relativity to Strings>라는 강의를 들었다. 여러가지 흥미로운 이야기들이 있었지만, 강의 중에 했던 ‘사실상 chain rule이 모든 것을 다 한다’라는 말은 꽤나 인상깊었다. 필자 또한 물리를 공부하면서, 특히나 일반상대론을 공부하면서 chain rule이 얼마나 중요한 기초인지를 매번 깨닫는다. 이번 포스팅에서는 그토록 중요한 chain rule이 직교좌표계가 아닌 경우에도 식$(2)$와 같은 형태가 변하지 않는다는 사실을 설명해보려 한다.
우선 먼저, ‘비스듬한 좌표계를 다룰 필요성’에 대해 간략히 논해보자. 종이나 칠판과 같은 2차원 평면에서 일어나는 무언가를 기술하기 위해선, 당연히 독립된 두개의 축을 택하는것이 편하다. 하지만 굽어있는 공간에선 ‘모든 공간에 적용되는 직교좌표계’자체가 존재하지 않는경우가 많다. covector를 다룬 지난 포스팅에서 설명했듯, 굽어있는 공간은 모든 면을 정사각형 타일로 빈틈없이 덮을 수가 없다. 아주 작은 일부는 가능하지만, 일반적으로 전체는 불가능하다1.
그래서, 어떤 임의의 점$P$ 주변의 평면으로 근사 할 수 있는 아주 작은 영역에서 다음과 같은 비스듬한 좌표계를 잡았다 해보자 :
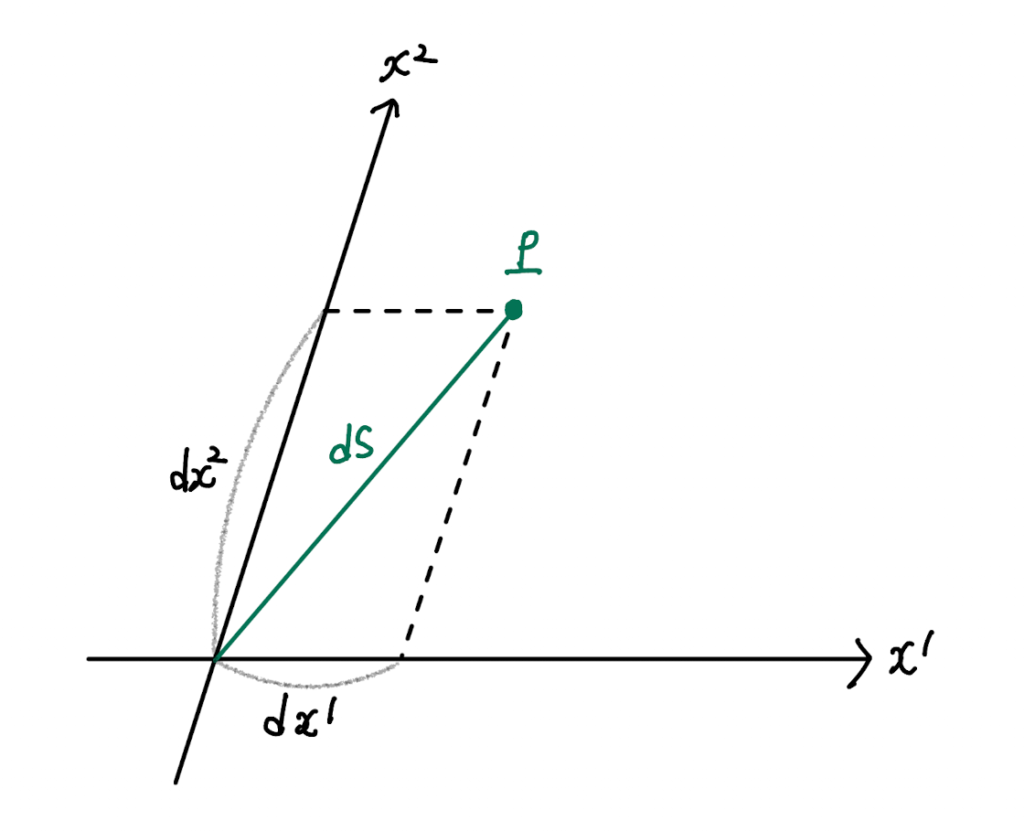
[그림#1]
이는 직교좌표계가 아니므로 $ds$의 제곱을 $dx^1$과 $dx^2$로 나타내려면 필히 $dx^1$와 $dx^2$간의 cross term이 발생한다. 하지만 식$(2)$의 형태는 기울어진 좌표계에서도 그런 cross term 없이 그대로 유지된다.
[그림#1]의 $ds$에 방향을 더해보자. 구면좌표계를 써서 원점$O$에서 $P$를 가리키는 단위벡터를 $\hat{r}$이라 하면, $\vec{OP}$는 다음과 같이 쓸 수 있다 : $$\vec{OP} =\hat{r} ds \tag{3}$$
그런데 $\vec{OP}$는 $x^1$축에 대한 단위벡터 $\hat{e}_1$과 $x^2$축에 대한 단위벡터 $\hat{e}_2$의 선형결합으로 표현 할 수도 있다 : $$\vec{OP} = dx^1\hat{e}_1+dx^2\hat{e}_2 \tag{4}$$
식$(3)$우변과 $(4)$우변을 등호 양쪽에 놓고 양변을 $\hat{r}$로 내적해주면 : $$ds = (\hat{r} \cdot \hat{e}_1)dx^1+(\hat{r} \cdot \hat{e}_2)dx^2 \tag{5}$$
이 때 $(\hat{r} \cdot \hat{e}_1)dx^1$는 $x^2$좌표는 고정하고 $x^1$만 $dx^1$만큼 움직였을때 $ds$가 얼마나 변하는지를 나타내므로, 이 자체가 편미분 $\frac{\partial s}{\partial x^1}dx^1$에 해당한다. 같은 이유로 $(\hat{r} \cdot \hat{e}_2)dx^2$를 편미분으로 나타내면 $\frac{\partial s}{\partial x^2}dx^2$이다 :
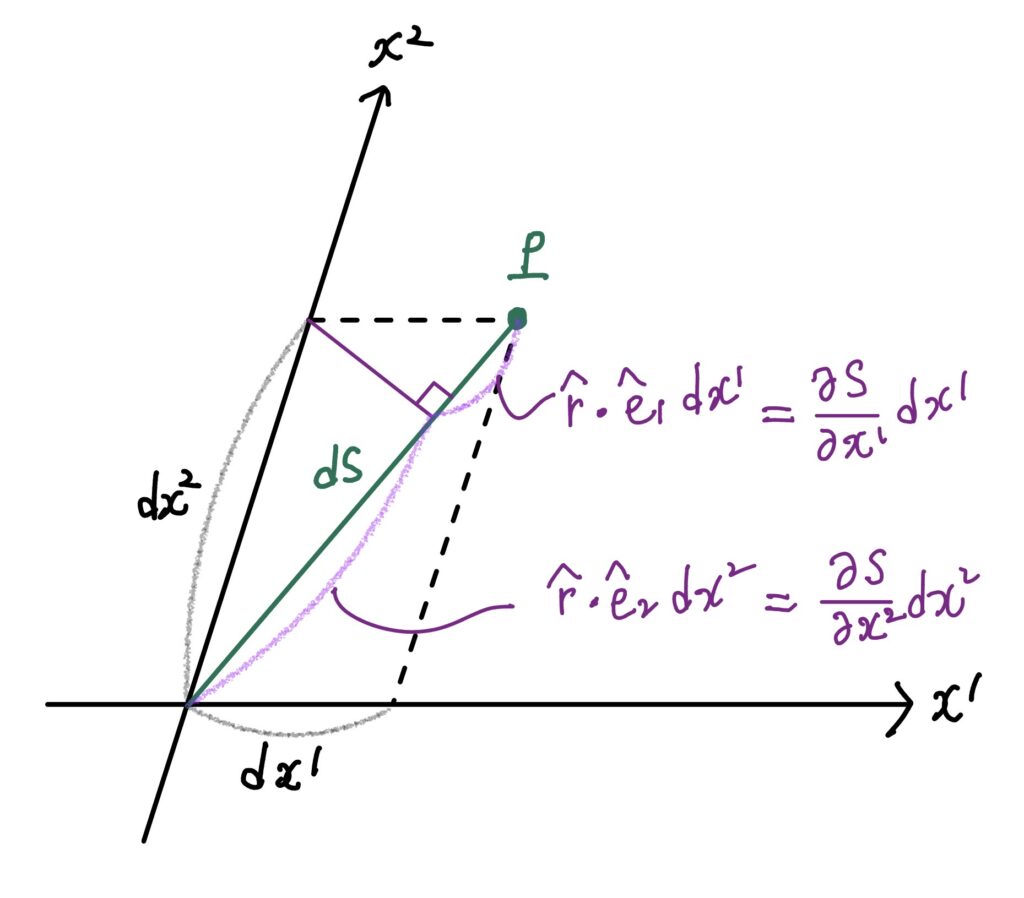
[그림#2]
따라서 $ds$는 비스듬한 좌표계 $(x^1, x^2)$에서도 $x^1$에 대한 편미분과 $x^2$에 대한 편미분의 선형결합으로 표현된다 : $$ds=\frac{\partial s}{\partial x^1}dx^1+\frac{\partial s}{\partial x^2}dx^2 \tag{6}$$
그리고 이런 표현식은 길이 $s$뿐만 아니라 어떤 부드러운 임의의 함수 $f$에 대해서도 마찬가지이다. 사실 앞서 한 $s$에 대한 분석은, 함수 $f(x,y)=\sqrt{x^2+y^2}$를 원점 부근에서 분석한것이나 다름없다. 그런데 이때 $f$를 원형좌표계로 표현하면 그저 $\sqrt{x^2+y^2}=r$이다. 즉 $f$는 원점에서 얼마나 많이 떨어져있든 선형적으로 증가하므로, 사실 원점부근이 아니라 다른 어디를 잡아도 식$(6)$과 같은 선형적 분석이 가능하다.
만약 함수$f(x,y)$가 $xy$평면 위에서 울렁거리면서 변하는 곡면이라면, 식$(6)$과 같은 분석은 그 곡면이 충분히 평면같아 보이는 어떤 임의의 점$(x,y)$ 근방에서만 성립한다. 하지만 어쨋든 그런 조건이라면, 어떤 국소적인 영역하에선-마치 약1m 크기의 우리가 반지름 6,371km인 지구를 평평하다고 느끼듯- $f(x,y)$는 평면과 같을 것이고 결국 그런 조건하에선 어떤 함수든 식$(6)$과 같이 성분들을 선형적으로 나눌 수 있다.
또한, 위에서는 2차원 화면에서 설명하기 위해 2차원을 택했지만 굳이 그럴 필요도 없다. 결국 식$(6)$을 임의의 $N$차원에 존재하는 어떤 부드러운 함수 $f$에 대해 써보면 : $$df(x^1, x^2, \cdots , x^N)=\frac{\partial f}{\partial x^{\mu}}dx^{\mu} \tag{7}$$
이런 수학적 구조는 좌표를 변환 할 때도 그대로 유지된다. 예를들어 [그림#2]의 상황을 원점은 같지만 다른 식으로 기울어진 두 축 $(y^1,y^2)$상에서 분석한다고 해보자. 그렇다면, 우리가 $ds$를 식$(6)$에서 $x^1$과 $x^2$의 성분으로 나눴듯 $dx^1$과 $dx^2$ 또한 정확히 같은 원리로 그 다른 축에 대해 다음과 같이 전개된다 : $$\left\{ \begin{aligned} dx^1 &= \frac{\partial x^1}{\partial y^1} dy^1 + \frac{\partial x^1}{\partial y^2} dy^2 \\[1em] dx^2 &= \frac{\partial x^2}{\partial y^1} dy^1 + \frac{\partial x^2}{\partial y^2} dy^2 \end{aligned} \right. \tag{8}$$
식$(6)$에서 $s$ 대신 일반적인 함수를 뜻하는 $f$를 넣고, 또 $dx^{\mu}$ 자리에 식$(8)$의 결과를 대입해 보라. 또한 정확히 식$(6)$을 유도한 논리를 새로운 좌표$(y^1, y^2)$에 적용하면 다음과 같은 결과를 얻을 수 있는데 : $$df=\frac{\partial f}{\partial y^1}dy^1+\frac{\partial f}{\partial y^2}dy^2$$
그 두 결과를 비교하면 다음과 같은 식이 성립함을 알 수 있다 : $$\left\{ \begin{aligned} \frac{\partial f}{\partial y^1} &= \frac{\partial f}{\partial x^1} \frac{\partial x^1}{\partial y^1} + \frac{\partial f}{\partial x^2} \frac{\partial x^2}{\partial y^1} \\[1em] \frac{\partial f}{\partial y^2} &= \frac{\partial f}{\partial x^1} \frac{\partial x^1}{\partial y^2} + \frac{\partial f}{\partial x^2} \frac{\partial x^2}{\partial y^2} \end{aligned} \right. \tag{9}$$
지금까지 나온 수학적 형태들을 보면 느낄 수 있겠지만, chain rule을 쓰는것은 마치 completeness relation $\sum_{i} | x_i \rangle \langle x_i | = \mathbf{1}$을 아무데나 집어넣을 수 있는것과도 같다. 사실, 그 둘은 정확히 같은 개념의 서로 다른 표현이다.
식$(8)$의 형태는 다음과 같은 행렬로 나타낼 수도 있는데2 : $$\begin{pmatrix} dx^1 \\ dx^2 \end{pmatrix} = \begin{pmatrix} \frac{\partial x^1}{\partial y^1} & \frac{\partial x^1}{\partial y^2} \\ \frac{\partial x^2}{\partial y^1} & \frac{\partial x^2}{\partial y^2} \end{pmatrix} \begin{pmatrix} dy^1 \\ dy^2 \end{pmatrix} \tag{10}$$
보다 일반적으로 임의의 두 좌표계 ${x^i}$와 ${y^j}$에 대해서는 식$(10)$의 행렬식을 보다 간락히 다음과 같이 나타낼 수 있다 : $$dx^i = \frac{\partial x^i}{\partial y^j} dy^j \tag{11}$$
그렇다면, 거꾸로 $y$좌표계를 $x$좌표계로 표현한다면 그 형해는 다음과 같을 텐데 : $$dy^i = \frac{\partial y^i}{\partial x^j} dx^j \tag{12}$$
식$(12)$ 좌변의 $dy$를 식$(11)$ 우변에 집어넣으면, 결과적으로 $x$를 $y$에 대해 표현했다가 다시 $y$를 $x$로 표현하는것이니, 그 결과는 자기자신이 나와야 한다. 따라서 행렬 $\frac{\partial x}{\partial y}$와 $\frac{\partial y}{\partial x}$는 서로 역행렬 관계에 있다는걸 알 수 있다 : $$\frac{\partial x^i}{\partial y^k} \frac{\partial y^k}{\partial x^j} = \delta^{i}_j$$
기왕 하는김에, 이런 수학적 형태를 한 단계만 더 깊이 발전시켜보자. 식$(1.5)$와 식$(7)$의 우변은 $df$로 같다. 그렇다면 어떻게 $\nabla f$와 $d\vec{s}$를 basis까지 표현된 정확한 벡터로 쓸 수 있을까? 본 글 초두에 소개했던 지난 포스팅에서는 모든 계산을 비교적 낱낱히 써가며 설명했는데, 이번에는 아인슈타인의 덧셈 notation의 형태를 통해 추론하는 식으로 해보자.
고등학생들은 자연수에 대한 지수의 곱셈법칙 – 예를들어 $3^m \times 3^n = 3^{m+n}$ – 을 배우고 나서 엄밀한 증명없이 그 규칙을 실수영역으로 확장 할 수 있다. 이는 지수연산 규칙이 그만큼 강력한 수학적 형태이기 때문인데, 마찬가지로 아인슈타인의 덧셈규칙은 윗/아랫 첨자를 다루는데 너무나 강력하고 효율적인 규칙이다. 따라서 지금 우리와 같은 상황에선 그 형태를 지켜주는것 만으로도 옳은 답을 즉각 도출 할 수 있다.
식$(1.5)$과 식$(7)$을 비교해보면, 분명 $\nabla f$는 $x^{\mu}$의 편미분 $\frac{\partial f}{\partial x^{\mu}}$들로 이루어져 있다. 그런데 분명 $f$의 gradient – 즉 $\nabla f$는 벡터이며, 동시에 이는 index를 가지고 있지 않다. 이는 곧 component $\frac{\partial f}{\partial x^{\mu}}$와 뭔지모를 basis가 contract 되어있음을 뜻한다. 그런데 이때 $\frac{\partial f}{\partial x^{\mu}}$는 $x^{\mu}$가 분모에 들어가 있으므로, 이는 lower index에 해당한다. 따라서 이것이 아인슈타인 덧셈규칙 하에서 곱해져 summation이 되려면 upper index가 붙은 basis가 필요하다. 이렇게 단순히 아인슈타인 덧셈규칙을 지킴으로써, 우리는 다음과 같은 형태가 성립함을 알 수 있다 : $$\nabla f = \frac{\partial f}{\partial x^{\mu}} \hat{e}^{\mu}$$
정확히 같은 논리를 $ds$에 적용해보면 다음과 같은 결론에 이르게 된다 : $$d\vec{s} = dx^{\nu} \hat{e}_{\nu}$$
지난 포스팅에서 설명했듯 $\hat{e}_{\mu} \cdot \hat{e}^{\nu} = \delta^{\nu}_{\mu}$이므로, 벡터형태로 표시된 $\nabla f$와 $d\vec{s}$를 통해 $df$를 계산하면 다음과 같다 : $$\begin{aligned} df &= \nabla f \cdot d\vec{s} \\ &= \left( \frac{\partial f}{\partial x^\mu} \hat{e}^\mu \right) \cdot \left( dx^\nu \hat{e}_\nu \right) \\ &= \frac{\partial f}{\partial x^\mu} dx^\nu \underbrace{\hat{e}^\mu \cdot \hat{e}_\nu}_{\delta^\mu_\nu} \\ &= \frac{\partial f}{\partial x^\mu} dx^\mu \end{aligned}$$
그리고 $\hat{e}^{\mu}=g^{\mu\nu}\hat{e}_{\nu}$이므로, $\nabla f$는 다음과 같이 표현 할 수도 있다 : $$\nabla f = g^{\mu\nu} \frac{\partial f}{\partial x^{\mu}} \hat{e}_{\nu}$$
직교좌표계에서는 $g^{\mu\mu}$가 단위행렬이고, 또 그땐 co-basis와 contra-basis가 정확히 같기 때문에 윗첨자/아랫첨자도 필요없고 metric tensor도 필요없다. 하지만 기울어진 좌표에서는 그런 일종의 ‘degeneracy’가 깨진다. 그리고 그런 상황에선 머릿속에서 chain rule 같은 규칙도 흔들릴 수 있다. 따라서 이번 포스팅과 같은 훈련이 필요하다. 이런 연습이 없으면 chain rule이나 upper/lower index 같은 것들이 엄청나게 헷갈릴 수 있다.
■
- 사실, 그렇게 모든 영역에서 직교좌표게를 설명할 수 있는 공간을 ‘manifold’라고 부른다. 관련하여 필자가 읽은 좋은 글 한편을 소개한다 : <What Is a Manifold?> (2025 Nov, Quanta Magazine) [^]
- 참고로 식$(10)$에서 편미분으로 이루어진 행렬은 일반적으로 ‘자코비안 행렬Jacobian matrix’라고 불뤼는 행렬의 한 예이다. [^]