양자역학에서 손으로 완벽하게 풀 수 있는 문제는 그다지 많지 않다. 하지만 물리 전공자들이 반드시 배워야 하는 세가지 경우가 있는데, 그것은 바로 무한사각우물infinite square well, 조화진동자harmonic oscillator , 수소원자hydrogen atom 이다. 특히나 infinite square well은 다른 경우에 비해 수학적 난이도가 매우 낮아 고등학생에게도 가르칠 수 있을 정도인데, 이번 포스팅에선 그 연장선상에 있는 delta function potential 문제를 풀어보려 한다.
delta function $\delta(x-x_0)$은 $x=x_0$에서만 무한대의 값을 가지고 다른 곳에선 $0$이며 그래프 면적이 1인 함수이다. 이 함수는 공간상에서 점입자를 나타내는 등의 방식으로 물리에서 아주 일반적으로 쓰인다. delta function을 수학적으로 나타내는덴 여러가지 정의가 있을 수 있지만, 이를 무한히 좁고 무한히 높은 직사각형으로 보는것은 개념적으로나 수학적으로나 대단히 유용한 정의이다. 보다 구체적으로 말하자면, $\delta(x-x_0)$은 무한히 작은 양의 실수 $\epsilon$에 대해 $x_0$을 중심으로 $\pm \frac{\epsilon}{2}$ 영역에 걸쳐 $\frac{1}{\epsilon}$의 값을 가지는 상수함수로 취급 할 수 있다.
양자역학에선, 입자가 느끼는 potential이 1차원 delta function 아랫쪽으로 꺼져있으면 potential well이 되고, 위쪽으로 서있으면 potential barrier가 된다 :
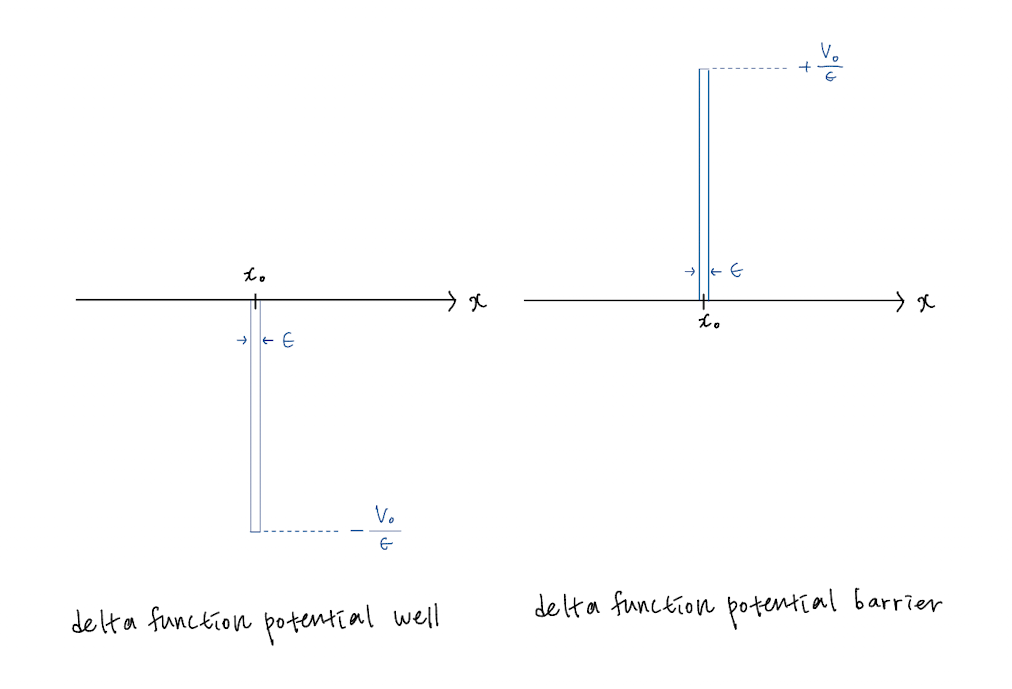
먼저 well에 대한 문제를 풀어보자. 전자의 에너지가 0보다 크다면, 이는 마치 전자의 파동이 왼쪽에서 오른쪽으로 진행하다 너비가 아주 얇으며 아래로 꺼진 방지턱을 지나는 것과 비슷하다. 이때 전자의 파동 일부는 앞으로 그대로 진행하고 일부는 뒤쪽으로 반사될것이다1.
하지만 이번 포스팅에서 다루고자 하는 대상은 ‘정상상태stationary state’ — 즉 시간에 따라 변하지 않는 상태를 다루고자 한다2. 이 경우 슈뢰딩거방정식 $$\left[ -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}-V_0 \delta(x-x_0)\right]\psi(x) = E\psi(x)$$으로 기술되는 전자의 에너지 $E$는 $-V_0<E<0$ 범위에 있다. 그런데 well 바깥에서는 potential이 그보다 큰 $0$으므로, 해당영역에서 전자는 $k=\frac{\sqrt{-2mE}}{\hbar^2}$의 scale을 가지고 expotentially decay 하는 형태로 존재한다 : $$ \psi(x) = \begin{cases} A e^{+k (x-x_0)} & (x < x_0) \\ A e^{-k (x-x_0)} & (x > x_0) \end{cases} $$
이때 양쪽 solution에 대한 coefficient가 $A$로 같은것은, $x=x_0$에서 파동함수를 연속으로 만들기 위함이다.
잠시 이런 답의 타당성을 따지기 위해, 몇가지 다른 가능성을 생각해보자. 순수하게 수학적으로 보자면 $x_0$ 양쪽에서 $\pm k$에 대한 solution이 다 나와야 하는게 맞지만, 물리적으로 보면 파동함수의 제곱은 그 아래에 유한한 면적을 가져야 하므로 무한대로 가면서 감쇠하는 녀석들만이 가능하다. 파동함수가 potential을 중심으로 현수선catenary의 뾰족한 부분이 $x_0$ 양쪽에 대칭적으로 솟아있는 – 마치 광안대교와 같은 형태로 존재 할 수도 있지 않겠냐 물을 수도 있겠지만, 그 또한 물리적으로 허용되지 않는다. 슈뢰딩거 방정식은 전자가 자유입자로 존재하는 delta-well 바깥쪽에선 파동함수 기울기가 불연속인 경우를 허용하지 않는다. 반대로 슈뢰딩거 방정식은 delta-potential이 있는곳에선 파동함수 기울기에 일정량의 불연속을 준다.
유한한 우물의 경우엔 왼/오른쪽 장벽에서 파동함수와 기울기가 모두 연속적으로 변한다. 하지만 delta-well은 장벽간 간격이 무한히 가까운 형태이며, 따라서 well의 양쪽 장벽을 부드럽게 이어주는 중간지대가 무한히 작은영역으로 축소되어있다고 볼 수도 있다. 따라서, 너비가 아주 얇은 well을 멀리서 보면 파동함수 기울기에 불연속이 있는것과 같은 이유로, delta-well은 본질적으로 파동함수 기울기에 일정량의 불연속을 준다.
불연속의 정도를 수학적으로 보다 정확하게 알기 위해선 슈뢰딩거 방정식을 $x_0 \pm \frac{\epsilon}{2}$에 대해 적분해주면 된다 : $$ \int_{x_0 – \frac{\epsilon_0}{2}}^{x_0 + \frac{\epsilon_0}{2}} dx \left[ -\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2} – V_0 \delta(x-x_0) \psi(x) = E \psi(x) \right] $$
이때 우변의 $E\psi(x)$는 유한한 양이 무한히 작은 영역에서 적분되니 $0$이 되고, 좌변 두번째 항에 대한 적분은 delta function의 일반적인 성질에 의해 $x_0$에서의 함수값 $-V_0 \psi(x_0) = -V_0 A$을 출력한다. 좌변 첫번째항의 적분은 파동함수의 일계미분 $\psi'(x)$에 대한 미분을 적분한것 이므로, 적분결과는 $- \frac{\hbar^2}{2m} \left[ \psi'(x_0 + \frac{\epsilon}{2}) – \psi'(x_0 – \frac{\epsilon}{2}) \right] = – \frac{\hbar^2}{2m} \Delta \psi'(x_0)$이다. 따라서 위식을 정리하면 : $$\Delta \psi'(x_0) = – \frac{2m V_0 A}{\hbar^2} \tag{1}$$
즉, delta-well의 정상stationary 파동함수는 야외 행사장의 몽골텐트마냥 $x_0$에서 뾰족하게 솟아있는 형태이다. 위 결과는 파동함수 기울기에 대한 불연속량이 음수라 말하고 있는데, 이는 타당하다. 불연속 지점 우측의 기울기는 음수이고 왼쪽의 기울기는 양수이니, 음수에서 양수를 빼면 그 결과는 음수이다. 직관적으로 볼때, 위 결과가 potential strength $V_0$에 비례한다는것 또한 옳다. 양자역학에서 운동량은 파동함수의 기울기에 비례한다. 포텐셜이 변하는 정도가 강하다는것은 해당 지점에서 강한 힘을 받는 것으로 볼 수 있으므로, 힘이 강할 수록 운동량 변화가 강하다는 것은 매우 자연스러운 결과이다3.
여기서 몇까지 짚어볼 부분이 있다. delta-potential이 단독으로 있지 않더라도, 어떤 임의의 정상상태 속에 delta-potential이 있다면 해당 지점에서 수식 $(1)$의 불연속은 성립한다. $(1)$에 대한 증명은, 그저 delta-potential이 존재하는 국소영역에 대해 슈뢰딩거 방정식을 적분 한 결과이다. 따라서 delta-potential이 어떤 다른 유한한 potential을 가지는 물리 system 속에 겹쳐져 있더라도 그런 수학적 분석은 동일한 결과를 낳는다.
이런 사실을 활용 할 수 있는 중요한 사례가 바로 에너지의 band struncture를 설명 할 때 나오는 dirac comb 문제이다. 이때는 delta-well이 아니라 delta-barrier가 등장하는데, 전자는 일정한 간격을 두고 무한히 뻗어있는 delta-barrier 속에서 어떤 종류의 정상상태를 형성 할 수 있으므로4 수식 $(1)$의 결과가 동일하게 성립한다.
다른 한가지 재미있는 점은 delta-well이 단 하나의 bound state만을 가진단 사실이다. 앞서 해당 bound state를 구하는 수학적 과정을 보면 우리가 구한 해가 유일하단걸 어렵지 않게 알 수 있다. 예를들어, delta-well에 대해 $\psi(-x)=-\psi(x)$인 반대칭antisymmetric 형태의 해가 가능한가? — 불가능하다. 전자는 $x_0$ 양쪽에서 자유입자로 존재하며, 따라서 파동함수는 $e^{\pm kx}$의 선형결합으로 나타내져야 한다. 하지만 앞서 말했듯, 이 둘의 선형결합으로 반대칭 파동함수를 만들려면 well 바깥쪽에서 파동함수 기울기가 불연속인 지점이 필연적으로 발생하며, 이는 자유입자에 대한 슈뢰딩거 방정식이 수학적으로 허용하지 않는 형태이다. delta-well에 대한 bound state는 우리가 구한 몽골텐트 형태만이 가능하다.
반면 유한한 너비 $L$을 가지는 infinite square well의 경우, 시스템은 무한히 많은 bound state와 그에 대응하는 무한히 많은 에너지 준위 $E=\frac{\hbar^2\pi^2n^2}{2mL^2}$를 가진다. 이는, well 면적이 유한하다는 조건하에서 $L$이 무한히 좁아진다면, 그땐 그 모든 에너지 준위가 하나의 bound state로 합쳐진다는 뜻이다5.
이것을 거꾸로 뒤집어 생각해보면, band gap 구조에 대한 훌륭한 insight를 얻을 수 있다. 너비 $L$의 유한한 potential well을 그 자체가 하나의 well이 아니라, 얇은 종이로 두꺼운 책을 만들듯 얇은 delta-well을 가로로 무한히 반복하여 연장한 결과라 생각해보라6. 우리는 delta-well과 infinite-well에 대한 슈뢰딩거 방정식을 정확히 풀 수 있다. 즉, 그렇게 delta-well을 무한히 붙여 확장한 결과, 하나의 에너지 준위가 무한히 많은 준위로 늘어남을 알 수 있는 것이다. 이것이 바로 불연속 에너지 준위를 가지는 원자들이 Avogadro number 만큼 모이면 band sturucture가 형성되는 원리이다. 일반적으로 특정 에너지 준위를 가지는 물리 시스템이 모이면, 그 원래의 준위는 모인 숫자에 비례하여 여러갈래로 갈라진다.
어떤 다른 potential의 극한을 취해 delta-well에 도달하는 것은 $\textrm{sech}^2$ 함수7로 표현되는 reflectionless potential을 통해서도 가능하다.
$V(x)=-V_0 \textrm{sech}^2(ax)$는 아랫쪽으로 볼록한 웅덩이 형태의 potential인데, 이는 신기하게도 ‘반사없는 우물’이다. 즉 왼쪽에서 들어온 자유입자가 $\textrm{sech}^2$ 우물을 지나가도, 분명 파동이 특정영역에서 힘을 받았음에도 불구하고 왼쪽으로의 반사가 일어나지 않는것이다. 이러한 scattering property와 더불어, 이에대한 bound state를 수학적으로 정확히 풀어보는것은 꽤나 도전적인 과제인데, 필자는 학부시절, 인턴으로 들어간 한 이론물리 연구실에서 이를 연구주제 삼아 깊이 공부한적이 있다. 이와 관련하여 Griffiths 양자역학교재에 연습문제가 하나 있는데, 관심있다면 한번 도전해보시기 바란다 :

Griffiths 양자역학 3판 Problem #2.52
나는 reflection potential 문제를 풀면서, 이에 대한 극한을 취함으로써 delta-well과 harmonic oscillator에 대한 결과를 reproduce 해보려 했었다. 오래전 일이라 기억이 흐릿한데 ··· 아마 delta-well은 비교적 쉽게 되었는데, harmonic osciilator는 이리저리 해보다가 안되어서 포기했던걸로 기억한다8. 외장하드를 뒤져보니 당시 만들었던 포스터가 있는데, $\textrm{sech}^2$ potential의 exact solution을 찾는 방법과 몇가지 재미있는 분석들이 있다 :
■
- 이런 delta-well에 대한 산란문제는 Griffiths 양자역학 교과서 3판 2.5.2절에 상세히 설명되어있다. 결과만 살펴보자면, 이 때 반사확률 $R$과 통과확률 $T$는 다음과 같다 : $R=\frac{1}{1+\frac{2\hbar^2E}{mV_0^2}}$, $T=\frac{1}{1+\frac{mV_0^2}{2\hbar^2E}}$[^]
- 이렇게 필자 마음대로 대상을 한정하는데 있어서 독자들께 꽤나 죄송한 마음이 든다. 뭘 택해서 설명 할건지는 전적으로 필자의 상황 속에서 결정되는데, 사실 이런 포스팅은 더 길고 완결성있는 교과서를 만들기 위한 준비작업이기도 하다.[^]
- 기울기 불연속에 대한 식을 통해 $k$의 값은 $\frac{mV_0}{\hbar^2}$임을 알 수 있다. $k$의 정의를 $E$에 대한 표현으로 바꾸면 bound state의 에너지는 다음과 같음을 알 수 있다 : $E=-\frac{mV_0^2}{2\hbar^2}$. 파동함수 normalization condition을 통해선 $A$이 값이 $\frac{\sqrt{mV_0}}{\hbar}$임을 알 수 있다.[^]
- Bloch’s theorm은 그런 격자 속 전자의 정상상태를 설명한다.[^]
- 이것이 delta-well의 bound state가 무한겹의 degenerated state란 뜻은 아니다. ‘$L$이 무한히 좁아진다’는 것은, 무한등분 되어있는 delta-well을 한지점에 중첩시킨다는 뜻이 아니다. 만약 그렇게 본다면 그 중첩의 결과는 유한한 면적의 delta function이 아니라 면적 $\frac{1}{\epsilon} \times \infty$ — 즉 무한히 좁은 영역에서 무한한 면적을 가지는 함수가 된다. ‘$L$이 무한히 좁아진다’는 것은, finite potential을 delta-well이 가로로 무한히 겹쳐진 결과라 보았을때 — 그 때를 기준으로 delta-well을 계속해서 제거해 결국 하나만 남긴다는 뜻이다. 달리 말하자면 이렇다 : delta-well을 원자와 같은 불가분의 최소 단위로 본다면, 그것이 가지는 정상상태는 하나이다. 그리고 그 원자가 무한히 모이면 무한히 많은 에너지 준위를 만들어 낸다. 실제 세계에서 원자는 무한히 많지 않은데, 보통 원자 $N$개가 모이면 기존의 준위 하나는 $N$개로 갈라진다.[^]
- 이 상황을 보다 엄밀하게 다루려면, 각각의 potential이 겹치는 부분에 대해 세심한 주의가 필요하다. potential well을 어떤 한점에서 불연속적으로 내려갔다가 일정거리만큼 평평하다 다시 불연속적으로 올라가는 형태로 생각한다면, 그런 potential well 두개를 나란히 겹칠땐 겹쳐지는 point에서의 potential 값은 수학적으로 잘 정의되지 않는다. 그 부분에서의 값을 $0$이라 하든 $-V_0$라 하든, 그런 식으로는 well 내부에서 일정한 값을 가지게 할 수 없다. 뭐, $-\frac{V_0}{2}$라고 두는것은 훌륭한 방안처럼 보이지만, 함수를 연속적인 형태로 다루길 원한다는 다른 식의 접근이 필요하다. 이런 문제를 해결하려면 delta-well을 직사각형이 아니라 이등변 삼각형으로 다루면 된다. 어차피 delta-well을 좁고 긴 직사각형으로 본건, 쉬운 분석을 위한 자의적 정의였다. delta function은 그것의 일반적인 수학적 정의만 유지된다면 다른 어떤 형태로 분석해도 무방하다. 따라서 delta-well을 이등변삼각형으로 두고 하나의 well의 peak와 그 옆 well의 시작점이 겹쳐지게 가로로 쌓는다면 그 결과는 유한한 너비를 가지는 finite potential well이 될 수 있다.[^]
- $\textrm{sech}$는 $\textrm{cosh}$ 함수의 역수이다 : $\textrm{sech}(x) = \frac{2}{e^x+e^{-x}}$[^]
- $\textrm{sech}^2$ 포텐셜의 parameter들을 이리저리 조절하여 harmonic oscillator에 최대한 가깝게 만들면 bound state 에너지 준위가 등간격을 이룰것이다. 그런 직관을 수학적으로 엄밀히 보이려 했었는데, 생각보다 쉽지 않았던걸로 기억한다.[^]