간단한 예시를 통한 covector의 이해

학교에서는 언제나 ‘직교좌표계’를 가르친다 :

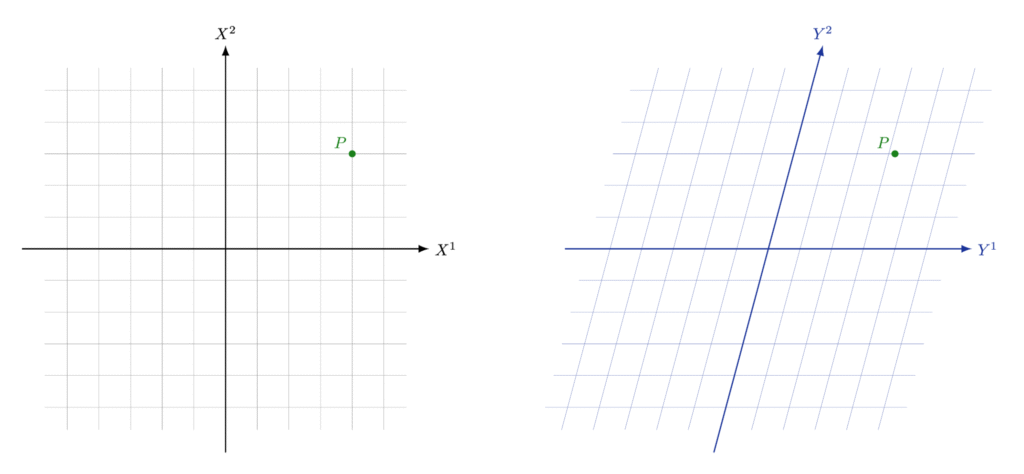
Fig#1. 직교좌표계 $ (X^1, X^2) $와 기울어진 좌표계 $ (Y^1, Y^2) $

고등학교는 당연하고, 대학에서도 임의의 점 $P$를 Fig#1의 $Y$ 좌표계처럼 기울어진 좌표계에 놓고 설명하는 경우는 거의 없다. …그런데 그래야 할 필요가 있을까? 기울어진 좌표는 이해하기 어렵다. 예를들어 $X$ 좌표계에서 원점과 점$P$ 사이의 거리제곱을 계산하려면, 그저 $X^1$ 좌표와 $X^2$ 좌표를 각각 제곱해서 더해주면된다. 하지만 $Y$ 좌표계 에서는 그렇지 않다. 좌표의 첨자가 정확히 지수자리에 들어간다는 것도 혼란을 가중시킨다. 하지만 직교좌표계만으로는 우리가 살고 있는 굽은 시공간을 이해 할 수 없다. 반드시 기울어진 좌표계를 이해해야 한다.

이번 포스팅의 목적은 co-vector를 직관적으로 이해해 보는것이다. 하지만 그 개념이 어떤 맥락에서 나온 것인지를 먼저 알 필요가 있다. 구shpere의 표면을 한번 생각해보자 :

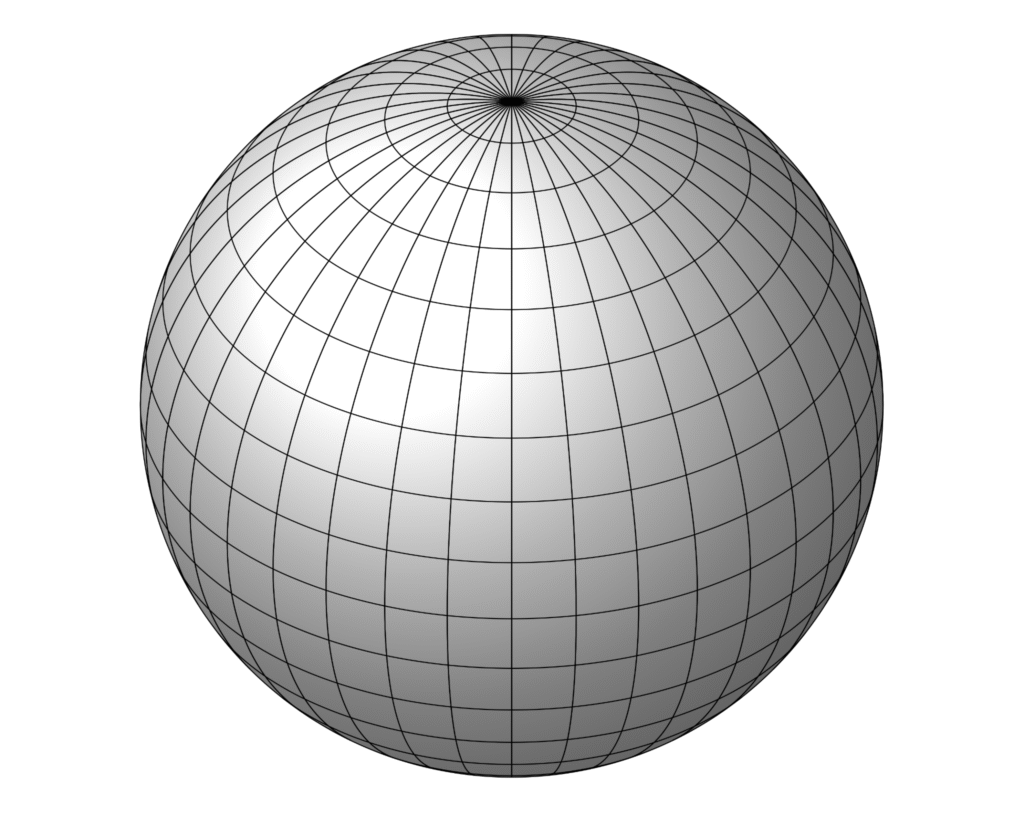
Fig#2. surface of the 2D sphere

우리는 학교에서 지구가 둥글다는 사실을 배우지만, 일상생활에서 지구의 곡률을 몸소 느낄 일은 사실상 없다. 학교 운동장에만 나가봐도 그렇다. 지구는 둥글다지만, 학교 운동장은 평평하다. 즉, 굽어있는 공간이라도 충분히 작은 스케일에서는 평평해 보일 수 있다. 그리고 그 평평한 공간에선 Fig#1의 $X$좌표계 처럼 직교좌표계를 그려볼 수 있다.

만약 지구가 평평하다면, 그렇게 어떤 임의의 지점에서 그린 직교좌표계의 격자 하나하나는 완전한 정사각형의 형태를 끝까지 유지 할 것이다. 즉, 지구가 평면이라면 정사각형 타일로 모든 영역을 빈틈없이 매울 수 있는것이다. 하지만 실제론 그렇지 않다. 만약 Fig#2 처럼 적도의 어떤 영역에서 타일을 채워나가기 시작한다면, 극지방으로 올라갈 수록 타일은 점점 더 비대칭적인 평행사변형이 된다. 결국 극지방에서는 삼각형 타일을 써야 한다. 그래야 구sphere의 모든 면을 빈틈없이 매울 수 있다. 만약 북극에서 부터 정사각형 타일로 채워나간다면 적도에선 삼각형 타일을 써야 한다. 그 어디를 기준으로 잡더라도, 굽은 공간에서는 모든 영역을 정사각 타일로 채울 수 없다. 그리고 이것이 바로 ‘기울어진 좌표계’가 굽어있는 공간 또는 시공간 의 기술에 필수인 이유다. 굽은 공간의 어떤 국소 영역에선 직교좌표계를 잡을 수 있지만, 그 선들의 직교성은 공간을 채워나가며 틀어지게 된다¹.

기울어진 좌표계의 필요성은 이 정도 개념적 설명으로 마치고, 그것을 수학적으로 어떻게 표현할지에 대해 생각해보자. 일단 성분들에 대한 직접적 비교를 위해 $X$와 $Y$ 좌표계를 겹쳐놔 보자 :

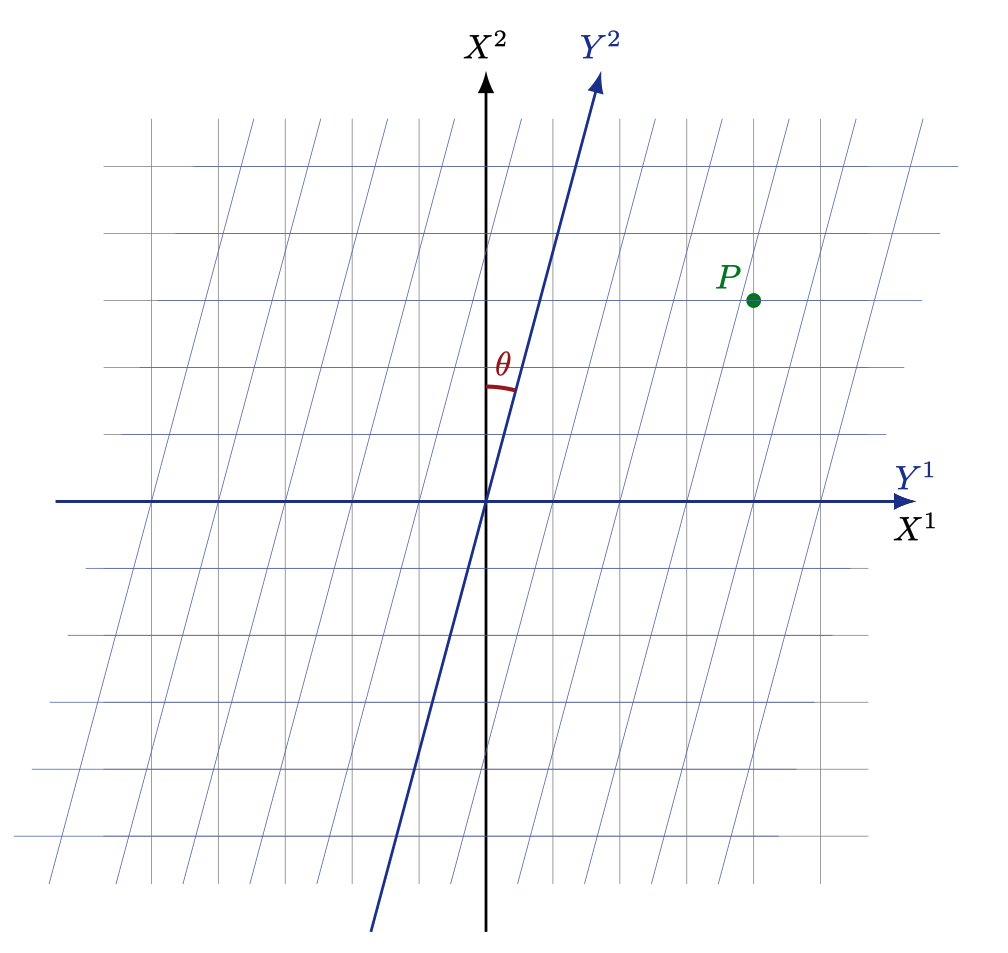
Fig#3. 겹쳐진 $X$와 $Y$ 좌표계

두 좌표계는 $P$를 각각 다른 성분으로 읽어내는데, $ (X^1(P), X^2(P))$와 $ (Y^1(P), Y^2(P))$간의 관계는 다음과 같이 각 성분들이 나타내는 길이를 모두 모아놓고 보면 기하적으로 계산 해 볼 수 있다 :

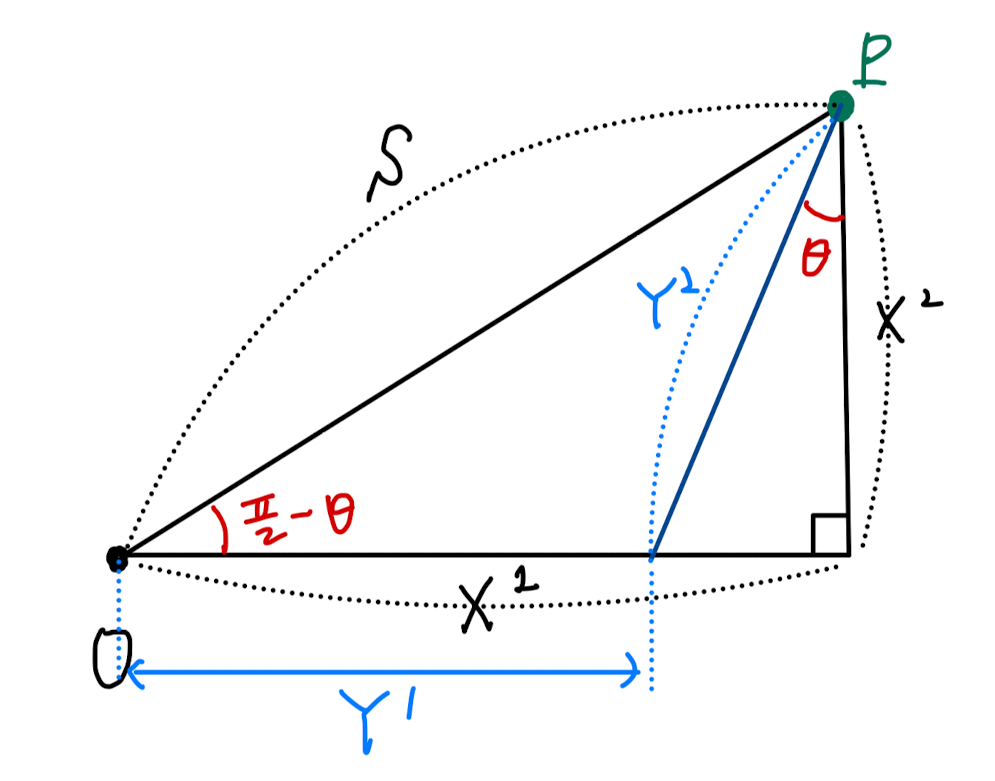
Fig#4.

앞서 언급했듯, 좌표성분에 대한 labelling number를 지수자리에 숫자를 넣어 표시하는 방법엔 오해의 소지가 있다. Fig#4에서 $X^2$는 $X$를 두번 곱한다는 뜻이 아니라, 점 $P$를 $X$좌표계에서 나타냈을때 두번째 좌표 성분이라는 뜻이다. 하지만 이런 표기법엔 그런 오해의 여지를 감수하고서라도 얻는 이점이 더 많다. 그래도 이런 표기가 처음이고 익숙치 않다면 주의 할 필요가 있다.

위 도형을 보면서, $X^1$과 $X^2$가 어떻게 $Y^1$과 $Y^2$를 통해 나타낼 수 있는지 생각해 보자 : $$Y^1 = X^1 – Y^2 \sin\theta, \quad X^2 = Y^2 \cos\theta \to \begin{pmatrix} X^1 \\ X^2 \end{pmatrix} = \begin{pmatrix} 1 & \sin\theta \\ 0 & \cos\theta \end{pmatrix} \begin{pmatrix} Y^1 \\ Y^2 \end{pmatrix} \tag{1}$$

원점 $O$와 점 $P$사이의 거리 $S$를 $X$성분으로 나타내면 : $S^2 = (X^1)^2+(X^2)^2$. 이는 익숙히 알고 있는 피타고라스 정리 그대로이다. 그런데 이를 $Y$좌표의 성분으로 나타내면 어떻게 될까? 식 (1)을 사용하면 : $$\begin{aligned} S^2 &= (X^1)^2 + (X^2)^2 \\ &= (Y^1 + Y^2\sin\theta)^2 + (Y^2 \cos\theta)^2 \\ &= (Y^1)^2 + (Y^2)^2 + 2 Y^1 Y^2 \sin\theta \end{aligned}$$

그러니까, $S^2$을 $X$좌표계에서 나타내면 $ (X^1)^2+(X^2)^2$이고, $Y$좌표계에서 나타내면 $ (Y^1)^2 + (Y^2)^2 + 2 Y^1 Y^2 \sin\theta$ 이다. 그런데, $S^2$을 나타내는데 있어 모든 좌표계를 아우르는 일반적인 표현법은 없을까?

$S^2 (X^1, X^2$)와 $S^2 (Y^1, Y^2)$는 다음과 같이 쓸 수도 있다 : $$\begin{aligned} S^2(X^1, X^2) &= 1 \times X^1 X^1 + 0 \times X^1 X^2 + 1 \times X^2 X^1 + 0 \times X^2 X^2 \\ S^2(Y^1, Y^2) &= 1 \times Y^1 Y^1 + \sin\theta \times Y^1 Y^2 + \sin\theta \times Y^2 Y^1 + 1 \times Y^2 Y^2 \end{aligned}$$

그리고 이는 모두, 다음과 같은 급수형태를 공유한다 : $S^2 = \sum_{\nu=1}^{2} \sum_{\mu=1}^{2} A_{\mu\nu} B^{\mu} B^{\nu}$. ‘아랫첨자와 윗첨자가 반복되면 모든 index에 대해 summation을 해준다’는 rule²을 적용하면, 이는 다음과 같이 더 간단하게 표현 할 수 있다 : $$S^2 = g_{\mu\nu} X^{\mu} X^{\nu} = g’_{\mu\nu} Y^{\mu} Y^{\nu} \quad \text{where} \quad g_{\mu\nu} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \ g’_{\mu\nu} = \begin{pmatrix} 1 & \sin\theta \\ \sin\theta & 1 \end{pmatrix} \tag{2}$$

이 개념을 자연스럽게 확장해 보면, ‘co-vector’의 개념을 이해 할 수 있는데, 먼저 위치 벡터 $\mathbf{S}$를 $X$ 좌표계에서 나타내보자 : $\mathbf{S}=\hat{\mathbf{x}}_1X^1+\hat{\mathbf{x}}_2X^2 $. 위에서 윗첨자와 아랫첨자가 동일하면 해당 index에 대한 summation을 해줘야 한다 했는데, 이를 직관적으로 이해하기위해선 어떤 하나의 index가 행row이면 다른 하나의 index는 열column이라고 생각하는것이 좋다. 즉, $\mathbf{S}$는 $X$ 좌표에서 다음과 같이 행렬의 곱셈으로도 나타낼 수 있는 것이다 : $$\mathbf{S} = \hat{\mathbf{x}}_1X^1+\hat{\mathbf{x}}_2X^2=\left( \hat{\mathbf{x}}_1 \ \hat{\mathbf{x}}_2 \right) \begin{pmatrix} X^1 \\ X^2 \end{pmatrix}$$

만약 $\mathbf{S}$가 $Y$좌표계에서도 동일한 수학적 형태도 나타내어진다면 : $\mathbf{S}=\hat{\mathbf{y}}_1Y^1+\hat{\mathbf{y}}_2Y^2 $, $(\hat{\mathbf{x}}_1,\hat{\mathbf{x}}_2)$과 $(\hat{\mathbf{y}}_1,\hat{\mathbf{y}}_2)$ 사이엔 어떤 관계식이 성립되어야 할까?

그 답은 역시나 $\mathbf{S}$를 행렬의 곱 형태로 써놓고 보면 쉽게 알 수 있다. $\mathbf{S}=\hat{\mathbf{x}}_1X^1+\hat{\mathbf{x}}_2X^2 = \hat{\mathbf{y}}_1Y^1+\hat{\mathbf{y}}_2Y^2$ 이므로 이를 행렬 형태로 나타내면 : $$\left( \hat{\mathbf{x}}_1 \ \hat{\mathbf{x}}_2 \right) \begin{pmatrix} X^1 \\ X^2 \end{pmatrix} = \left( \hat{\mathbf{y}}_1 \ \hat{\mathbf{y}}_2 \right) \begin{pmatrix} Y^1 \\ Y^2 \end{pmatrix} \tag{3}$$

그런데 식(1)에서 보이듯 $X$좌표와 $Y$좌표의 관계는 다음과 같으므로 : $\begin{pmatrix} X^1 \\ X^2 \end{pmatrix} = \begin{pmatrix} 1 & \sin\theta \\ 0 & \cos\theta \end{pmatrix} \begin{pmatrix} Y^1 \\ Y^2 \end{pmatrix}$, 식(3)는 다음과 같이 다시 쓸 수 있다 : $$\left( \hat{\mathbf{x}}_1 \ \hat{\mathbf{x}}_2 \right) \begin{pmatrix} 1 & \sin\theta \\ 0 & \cos\theta \end{pmatrix} \begin{pmatrix} Y^1 \\ Y^2 \end{pmatrix} = \left( \hat{\mathbf{y}}_1 \ \hat{\mathbf{y}}_2 \right) \begin{pmatrix} Y^1 \\ Y^2 \end{pmatrix}$$

$Y$의 성분이 양변 오른쪽 동일하게 있으므로 등호가 성립하려면 그 앞부분이 같아야하고, 해당 부분을 전치transpose 시켜주면 : $$\begin{pmatrix} \hat{\mathbf{y}}_1 \\ \hat{\mathbf{y}}_2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} \hat{\mathbf{x}}_1 \\ \hat{\mathbf{x}}_2 \end{pmatrix} \tag{4}$$

따라서 $\hat{\mathbf{y}}_1 = \hat{\mathbf{x}}_1$이고 $\hat{\mathbf{y}}_2 = \hat{\mathbf{x}}_1\sin\theta +\hat{\mathbf{x}}_2\cos\theta$이다.

그런데 사실 Fig#4를 다시 보면, 이런 계산은 불필요하게 돌아온듯한 느낌도 든다. $\hat{\mathbf{x}}_1X^1+\hat{\mathbf{x}}_2X^2$는 원점에서 부터 시작해 오른쪽 수평으로 $X^1$ 만큼 간 후 위쪽 수직으로 $X^2$만큼 가면 점 $P$가 있다는 뜻이다. $\hat{\mathbf{y}}_1Y^1+\hat{\mathbf{y}}_2Y^2$는 — $\hat{\mathbf{y}}_1 = \hat{\mathbf{x}}_1$이므로 일단 첫번째 항은 원점에서 오른쪽 수평으로 $Y^1$ 만큼 가라는 뜻이다. 그리고 여기서 점 $P$에 도달하려면 ‘어떤 방향’으로 $Y^2$ 만큼 가야하는데, Fig#4를 보면 그 ‘어떤 방향’에 대한 단위 벡터가 바로 $\hat{\mathbf{x}}_1\sin\theta +\hat{\mathbf{x}}_2\cos\theta$이다. 따라서 식(4)의 결과는 이미 Fig#4에서 기하학적으로 읽어낼 수 있는 정보였던 것이다.

하지만 이번 포스팅의 목표는 이 간단한 예시를 통해 보다 일반적인 수학적 형태와 개념들을 유추하고 익히는 것이다. 우선 한가지 눈여겨 볼점은, 별도의 기하학적 분석없이 성분에 대한 변환식인 식(1)을 통해 기저의 변환식인 식(4)을 유도해낼 수 있었다는 사실이다. 사실 여기서도 ‘수학적 형태’의 위대한 힘을 엿볼 수 있다. 사실 $\theta$가 음수만 되어도 Fig#4와 같은 기하학적 분석은 더 골치아파진다. $\theta$ 뿐만아니라 성분들 또한 음수가 될 수 있는 일반적 상황이라면 상황은 더 심각해질 것이다. 하지만 놀라운 사실은, 다루는 모든 성분들이 양수였던 Fig#4를 통해 얻은 $X$좌표와 $Y$좌표 사이의 관계식은 임의의 $\theta$, 그리고 임의의 $P$에 대해 일반적으로 성립한다는 사실이다. 그리고 $2 \times 2$ 행렬로 나타내지는 그 하나의 관계식은 좌표성분과 기저 등, $X$좌표와 $Y$좌표 사이의 모든 관계를 함축적으로 담고있다.

또한 위의 분석만으로 metric tensor를 다르게 정의하는 법을 발견 할 수도 있다 : $g_{\mu\nu} = \hat{\mathbf{e}}_{\mu} \cdot \hat{\mathbf{e}}_{\nu}$. 이와 같은 정의를 식(4)에서 구한 결과에 적용하면 정확히 식(2)의 $g’_{\mu\nu}$가 계산된다는 것을 확인해보라. 식(2)에서 처럼 어떤 임의의 좌표계에서 길이가 어떻게 계산되는지를 통해 metric tensor를 정의 할 수도 있지만, 그것은 기저벡터의 내적을 통해서도 정의 할 수 있다. 그 두 정의는 수학적으로 동치이다.

그리고 우리는 여기서 자연스럽게 ‘co-vector’의 존재를 발견 할 수 있다. 식(2)에 나타난 다음의 수식을 잘 살펴보라 : $S^2=g’_{\mu\nu}Y^{\mu}Y^{\nu}$. 그리고 여기서 $g’_{\mu\nu}Y^{\mu}$는 $2 \times 2$ 행렬과 $2 \times 1$ 행렬의 곱이며, 그 계산결과는 $2 \times 1$ 행렬이다. 즉, $g’_{\mu\nu}Y^{\mu}$는 벡터 $Y^{\mu}$에 대한 선형변환인 것이다. 우리는 이 지점에서 아인슈타인의 덧셈규칙은 그 수학적 형태가 관련 개념을 직관적으로 잘 담고 있음을 확인 할 수 있다. $g’_{\mu\nu}Y^{\mu}$에서 아래/위로 반복되는 index인 $\mu$는 덧셈이 행해졌으니 사라질 것이고, 남아있는 index는 $\nu$ 밖에 없다. 따라서 $g’_{\mu\nu}Y^{\mu}$는 $Y_{\nu}$라고 표시하는 것이 합당하다 : $g’_{\mu\nu}Y^{\mu}=Y_{\nu}$. 이러한 수학적 규칙은 다른 어떤 텐서간의 곱에서도 동일하게 적용된다.

그렇다면 vector $\mathbf{S}$를 아랫첨자의 성분을 이용해서 표현해 볼 수 있다. 애초에 $\mathbf{S} = \left( \hat{\mathbf{y}}_1 \ \hat{\mathbf{y}}_2 \right) \begin{pmatrix} Y^1 \\ Y^2 \end{pmatrix}$ 였는데, $Y^{\mu} = (g’_{\mu\nu})^{-1}Y_{\nu}$이므로, $\mathbf{S}$는 다음과 같이 다시 쓸 수 있다 : $$\mathbf{S} = \left( \hat{\mathbf{y}}_1 \ \hat{\mathbf{y}}_2 \right) \frac{1}{\cos^2\theta} \begin{pmatrix} 1 & -\sin\theta \\ -\sin\theta & 1 \end{pmatrix} \begin{pmatrix} Y_1 \\ Y_2 \end{pmatrix}$$

여기서 $Y_{\nu}$ 앞부분을 $\hat{\mathbf{y}}^{\nu}$로 정의하면 $\mathbf{S}$는 다음과 같이 기저와 성분의 index 위치가 뒤집힌 형태로도 나타내질 수 있다 : $$\begin{aligned} \mathbf{S} &= \left( \hat{\mathbf{y}}_1 \ \hat{\mathbf{y}}_2 \right) \frac{1}{\cos^2\theta} \begin{pmatrix} 1 & -\sin\theta \\ -\sin\theta & 1 \end{pmatrix} \begin{pmatrix} Y^1 \\ Y^2 \end{pmatrix} \\ &= \left( \hat{\mathbf{y}}^1 \ \hat{\mathbf{y}}^2 \right) \begin{pmatrix} Y_1 \\ Y_2 \end{pmatrix} = \hat{\mathbf{y}}^1 Y_1 + \hat{\mathbf{y}}^2 Y_2 \end{aligned}$$

보통 $Y^{\nu}$를 그냥 ‘vector’라 부르고, $Y_{\nu}$를 ‘co-vector’라 부른다. 그리고 vector $Y^{\nu}$의 크기는 co-vector와의 내적을 통해 계산된다 : $S^2 = Y_{\nu}Y^{\nu}$. $X$ 좌표계에서는 metric tensor가 단위행렬 이었기 때문에 vetor와 co-vector가 일치한다. 따라서 $S^2=X_{\nu}X^{\nu}=X^{\nu}X^{\nu}$이다. 하지만 어떤 임의의 좌표계이든, 내적은 vector의 성분과 co-vector의 성분을 곱해서 더한것으로 나타내어진다.

여기서 한가지 중요한 사실은 vector에 대한 basis vector $\hat{\mathbf{y}}_{\mu}$와 co-vector에 대한 basis vector $\hat{\mathbf{y}}^{\nu}$의 tensor product가 단위행렬이라는 점이다 : $\hat{\mathbf{y}}_{\mu} \cdot \hat{\mathbf{y}}^{\nu} = \delta^{\nu}_{\mu}$. 위의 예시를 통해 실제로 이 관계식이 성립하는지 확인해보자. 그리고 좌표평면에서 $\hat{\mathbf{y}}_{\mu}$와 $\hat{\mathbf{y}}^{\nu}$를 함께 그려보라. $\hat{\mathbf{y}}_{\mu}$는 그 크기가 1이지만, $\hat{\mathbf{y}}^{\nu}$는 크기가 $\frac{1}{\cos^2 \theta}$ 이다.

$Y^{\nu}$를 보통 ‘contravariant component’라 부르고 $Y_{\nu}$는 ‘covariant component’라 부른다. 이는 $Y^{\nu}$는 coordinate basis $\hat{\mathbf{y}}_{\nu}$와 반대로 변하고 $Y_{\nu}$는 $\hat{\mathbf{y}}_{\nu}$와 동일하게 변하기 때문이다. 예를들어 $\hat{\mathbf{y}}_{\nu}$가 두배로 커졌다고 생각해보라. 기술하고자 하는 원래 vector $\mathbf{S}$는 그대로 있으므로, 그땐 $Y^{\nu}$의 크기가 절반으로 줄어야 한다. 그런데 $\hat{\mathbf{y}}_{\nu} \cdot \hat{\mathbf{y}}^{\mu} = \delta^{\mu}_{\nu}$ 이므로, $\hat{\mathbf{y}}_{\nu}$가 두배로 커지면 $\hat{\mathbf{y}}^{\nu}$는 두배로 작아져야 한다. 따라서 $\hat{\mathbf{y}}^{\nu}$에 대한 component인 $Y_{\nu}$는 두배로 커져야 한다. 그래야 그것이 동일한 vector $\mathbf{S}$에 대한 기술 일 수 있다.

■

엄밀하게 보면 이 설명은 문제가 있어 보인다. $Y$ 좌표계가 기울어 졌다는것은 metric tensor의 off-diagonal component를 통해 수학적으로 나타내어지는데, 2D sphere의 metric tensor엔 off-diagonal term이 없다 : $g_{\mu\nu} = \textrm{diag} (1, \sin^2\theta)$. 따라서 2D sphere에선 직교좌표계가 ‘기울어지는것’이 아니라 어느쪽 성분이 ‘찌그러드는것’ 이다. 우선 본문에선 굽은 공간을 기술하기 위해서는 직교좌표계를 넘어 좌표계에 대한 보다 일반적인 기술이 필요함을 개념적으로 전달하는 것을 목표로 삼았다. 여기서 개념의 효과적 전달과 수학적 엄밀성을 동시에 지키는 설명방법을 고안하기 위해선 고민의 시간이 좀 더 필요 할 것 같다.[^]
Einstein notation – Wikipedia[^]